The efficacy of a machine learning (ML) algorithm's learning capabilities is subjective to the quality and quantity of the data it is fed and the degree of magnitude of "useful information" that it contains.
What data features are important for machine learning projects or applications?
These data features (whether you have synthetic data sets, work with big data, have missing data gaps, labeled training data, etc.) will shape the model's algorithmic abilities to learn and in consequence, it is therefore critical to analyse and pre-process datasets before application to ensure data quality.
For machine learning projects, engineers must first assess all the data they have available, and answer the question 'how much data do I need?'.
The analysis of a dataset should produce key insights into the data quality and quantity, as well as its distribution.
Beyond this, long-term operation input data may also dynamically change with time. There are no guarantees that a user's data type or format will stay constant.
In the real-world application of machine learning, it is far from uncommon for datasets to diverge away from the picture-perfect data a machine learning model has been trained on.
how much data is needed for machine learning?
The cumulative effects of the mentioned factors hypothesise two beguiling questions, which nuances of a dataset quantify the quality of the data; and how much data do you need.
Knowing the quantity of data needed to train successful machine learning models does not come with a concrete analytical "equation" or "solution", rather answering this problem requires a series of paralleled logical conclusions to determine the feasibility of, dropping data, data augmentation, and finally what data to collect.
When building machine learning models, it is important for the model to have been exposed to a set of data points that represents a range of variation across the subspace of data.
This enables the model to generalise well to new inputs and more data.
This could be interpreted as has the dataset seen enough information or situations to be able to generalise to the real-world data it will be exposed to.
Expanding upon this, knowing the key functionality of the model you are using is of significant importance, as ML models can be used for a vast range of applications.
If the user has defined the model's key functionality or objective for example to be a classification or scalar extrapolation/interpolation, each objective generates a subset of individualised nuances regarding the data quantity.
A machine learning functionality must be defined in terms of the complexity of the problem relative to the training data variation and the complexity of the algorithm applied.
Using these logical metrics, I would like to present a set of thought experiments to validate the sensitivity of data quantity relative to functionality.
Beyond this, if understood, further clairvoyance of the fulcrum points between overfitting and underfitting phenomena can be achieved.
Deep learning problems
Consider an image classification problem between cats and dogs, the functionality of the model is to be able to correctly classify images, and the complexity of the model depends entirely on the quality and quantity of the images supplied.
Generally, using convolutional neural networks on relatively small sets of data (instead of big data) of images of cats and dogs have been shown to work quite well.
However, when the dataset is small, it also means the variation of examples will follow analogously. Though a small dataset can work quite well, it can form a mirage of overconfidence.
This is due to overfitting. Thus, with small sets of data in this functionality, the void of variety can lead to mistakes in classification.
To define this further, because of the small data variation, the model has become efficient at classifying from a limited dataset, but it is not well versed in data that it does not usually expect.
Expanding on this, if the ML model has only ever seen dogs that are white and small, it is all the model has fit to, so what would happen when the model is exposed to a dog that is larger and brown?
Even though the input is still a dog, it is likely that the ML model will not recognise it as such. Essentially a small dataset here has led to overfitting.
The model does not have the flexibility and guile to be able to recognise other dogs as its entire period of training exposure was centric to the contrary.
This presents a logical argument for expanding the dataset size, ideally towards an infinite number of images to build the most complete classifier, but this is not possible due to time and computational constraints.
Thus, logically adapting the expansion of the dataset to the specific problem is necessary, which requires agile human thought about what data to collect and imbed.
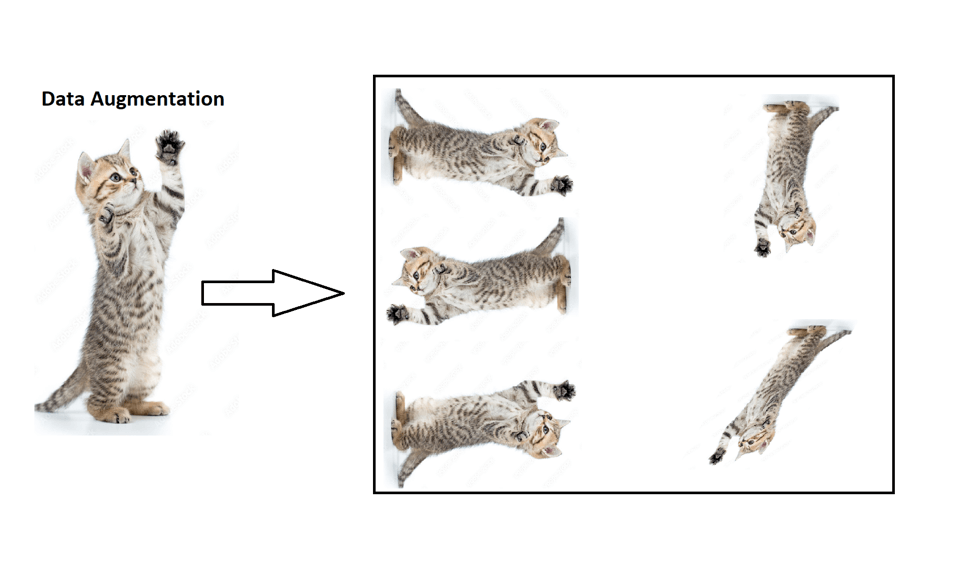
In the case of optimising smaller datasets where data collection is not feasible, concepts such as data augmentation exist.
For example, if all the images of the cats used to train the model were standing up, the model may fail to classify cats that are on all fours.
To solve this problem applying transformation techniques to rotate the orientation of images may solve this, as it will produce images of a reclined cat on all fours.
An expansion on this theme would be to integrate semi-supervised learning techniques which facilitate the generation of more data or images based on known inputs.
This can be implemented through the usage of GAN's which are optimised to produce feasible or "real" samples.
What if generating more data isn't feasible?
In circumstances where generating new data is not feasible, this allows for highly effective transfer learning approaches to be integrated.
This comprises of using a pre-trained network that has previously been trained on a larger scale dataset, where the pre-trained network can efficiently act as a generic model for the smaller network.
To conclude this thought experiment, if tactical data collection is not an option to diversify a dataset that may have to overfit to a small data sample, data augmentation methods do exist to optimise the dataset.
On the other hand, the problem scope can accomplish using a small dataset for technical streamlined problems.
Overall, this highlights the problem-specific nature of machine learning problems.
Machine learning with small data samples required
The fundamental nature of machine learning problems is the ability to find nuances and distinguished relationships with the raw data prior to feature engineering.
Generally, this phenomenon is more prominent with larger data sets that provide enough data to predict matches.
However, the idea of a large dataset is comparative, relative to the complexity of the architecture of the network being trained and the degrees of freedom that the problem presents.
Smaller datasets can be efficiently used in well-regularised ML models to encapsulate known physical phenomena and other interesting features if the problem task is well-defined.
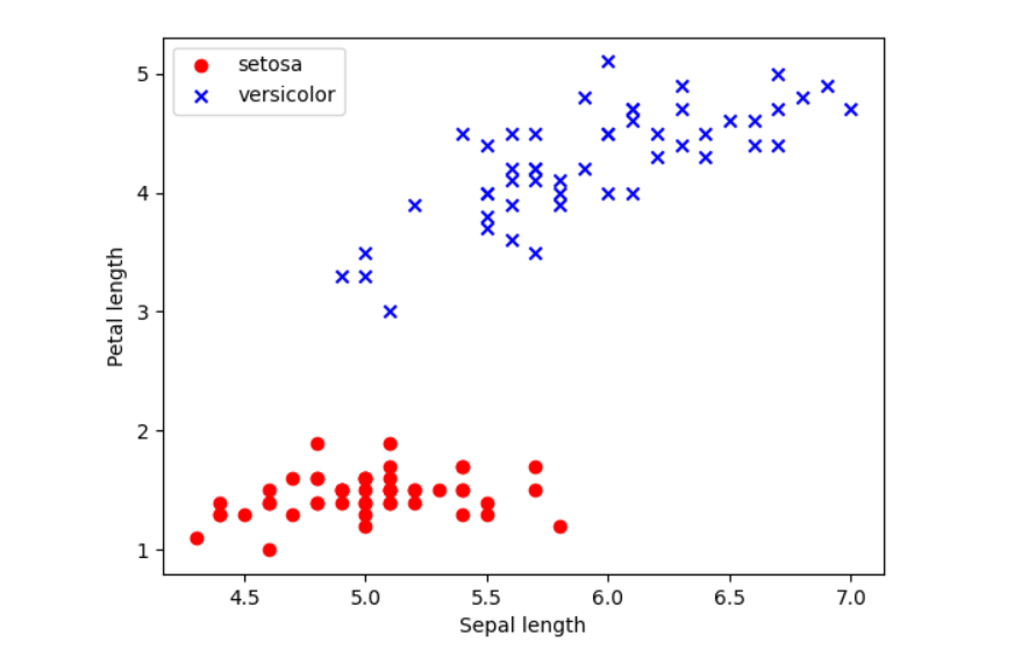
Having a well-defined problem can be subjective to the robustness of the correlative nature between features and labels or as simple as a well-defined distribution density. To explain this, I have plotted selected features from the IRIS dataset.
Consider applying K-nearest neighbours in this instance, where model performance is defined by distribution density. Even with 100 data points the decision boundary is evident, and the distribution is well-defined into distinctive agglomerated regions allowing for potential accurate predictions.
Machine learning for all types of data sets and data scientists
Consequentially, machine learning can be used in combination with different values in a small set of data; there are instances and different contexts where unique phenomena can be reproduced prolifically.
Understanding if the task at hand can be solved using sparse or small datasets combined with machine learning can only be understood or solved by applying the data, which supplements the user with the logical, statistical steps to take afterward if need be.
Therefore, the absence of a large dataset (big data) is not necessarily a barrier to entry for applying machine learning models. Instead, it presents the opportunity to learn more about your data and its nuances.
Ultimately, from an engineering and mathematic perspective, it presents a potential honeycomb of aesthetic data exploration which will enrich the engineers' understanding of their own data.
The relationship between data quality and data quantity
To begin to understand data quantity further, the relationship with data quality must be explored deeper. It is fundamental to recognise this relationship is a task-specific problem that requires human engineering.
There is no one answer for all; instead, the adequacy of a dataset will ultimately be defined by its ability to perform well at its given purpose.
The perturbations of a befitting, high-quality dataset on a business will be apparent through the escalation and optimisation of a host of facets.
For example, high-quality data will magnify a company's ability to make accurate and justified decisions with increased time efficiency.
The knock-on effect of this phenomenon encapsulates revenue amplification as a function of time and cost savings. Engineering a high-quality dataset involves fundamental pre-processing and "baked-in" human domain knowledge.
In particular deep learning studies involving neural networks are designed to help humans understand problems of heightened complexity and should encapsulate the physics and chemistry available that we know.
For deep learning applications, the data must enable the network to "stand on the shoulders of giants" adhering to the known physical phenomena and deciphering the unknown.
Data errors due to lack of data quality
The absence of data quality is a phenomenon that is excited from an array of real-world instances, including errors in data collection, erroneous\ non-contextual measurements, incomplete measurements, incorrect content, outliers and duplicate data.
Ultimately these conclude in placeholder strings such as NaN (not a number) or NULL representing unknown values commonly seen throughout datasets.
As mentioned, machine learning models are highly sensitive to the fed data, adding gravity to the necessity to process missing values before analysis. If these data points are simply ignored, it could lead to the models producing unexpected results.
Thankfully there exists a range of techniques available for a data scientist to galvanise models from falling victim to erroneous predictions using Pandas and Scikit-learn.
There exists a limited scope for dropping feature columns with missing data simply as they may contain data that has a high correlation with labels, i.e., high-quality data; thus, it becomes unfeasible to consistently drop columns.
To avoid this sad circumstance, a range of interpolation techniques exists such as mean imputation enabling missing values to be replaced with the column mean.
In addition, it is possible to interchange the mean with the mode value.
This choice relies on human intuition and domain knowledge providing an understanding of which transformation is the most logical.
To build upon this concept, real-world applications of machine learning concatenate categorical data and numerical data.
For example, machine learning applications in the medicinal sectors may use categorical features such as "male", "female", "benign", "malignant", "dormant", for which some machine learning model libraries will require categorical features to be encoded into integer values as not all estimators may achieve this conversion internally.
If the latter case exists, then the conversion to integer values may be achieved through pre-processing encoders. Ultimately this can improve the quality of the data for certain models.
Tightly intertwined with this concept exists data quality overfitting, a problem where models perform better on a training dataset than with a test dataset.
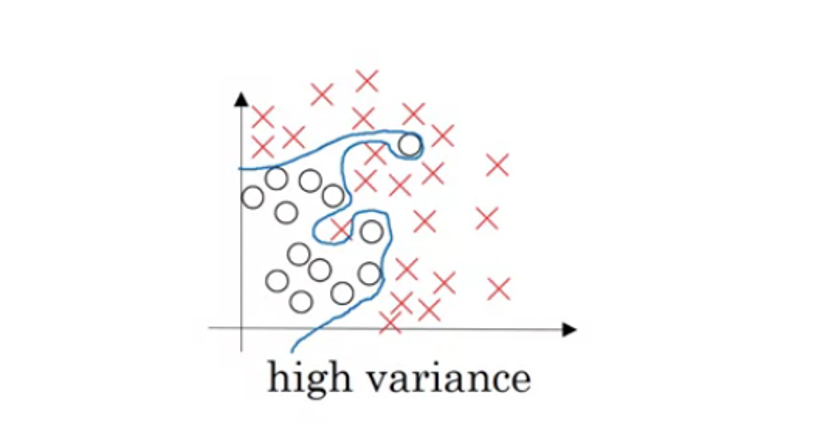
This can be summarised as the model failing to generalise to new unseen data giving the model a high variance.
High variance causes the algorithm to become significantly sensitive to minute changes in the input data thus making the model prone to modelling on random noise in the training data. Essentially the model is highly sensitive and far too complex for the training data.
An image below is attached to describe the phenomena of high variance, where the data is fit perfectly, illustrating the high sensitivity, complexity, and tendency to fit to random noise.
This training inaccuracy has various sets of solutions including expansion of the data set, and the introduction of regularisation, thus causing dimensionality reduction and producing a simpler model with fewer parameters.
Regularisation works by "zeroing" out the impact of hidden units throughout a neural network, hidden units are still used by the model, but they have a significantly smaller effect, consequently building a simpler model.
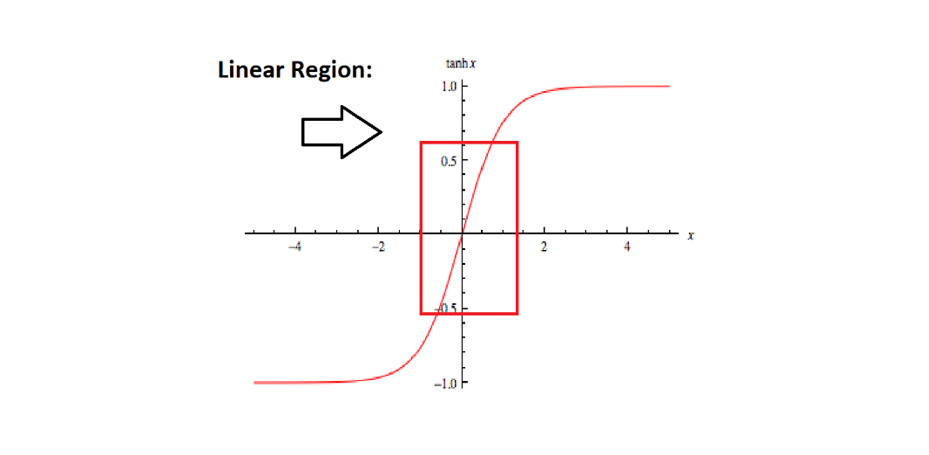
To build upon this further, when the weights in a neural network are minimised, mathematically, the values that enter the activation function are also minimised towards zero.
If this is visualised for classification problems using the sigmoid or inverse tan function where at the graph is linear, the activation values will be roughly linear. This phenomenon helps to generate a simpler, more linear network.
With unregularised models, dimensionality reduction can be used as a technique to reduce the complexity of a model overfitting to training data.
The zealous of feature selection algorithms is to select a subset of features relevant to the problem, thus augmenting computation efficiency through the removal of unrelated features/noise.
An example of a feature selection algorithm includes sequential backward selection, which subsequently phases out features from the full feature subset until the new subspace contains a desired number of features.
Improving data quality and employing machine learning techniques
In this article, we have seen that small datasets are not predestined as a barrier to entry for machine learning systems or applications, and you can get accurate results without large datasets.
Instead, small datasets or sample sizes present an exciting opportunity to learn more about your data, and how to augment and improve data quality logically.
To begin to understand the current feasibility of the data or sample size at stake, it must be propagated across a range of machine learning algorithms and explored thoroughly.
How to begin your own machine learning projects and improve data quality with Monolith AI
Monolith AI presents an intuitive artificial intelligence platform that enriches the engineer with a design space and hierarchy to understand where more data is needed to solve technical problems, while also quantifying the unique features already existing in the training data.
Beyond this, the Monolith platform also empowers the user with the correct tools to engineer their raw data, guiding the workflow through a series of transformations to enable models to achieve the highest accuracy possible.
What's more? This artificial intelligence (AI) platform allows one to transfer learning across their team, and be reused time and time again for another machine learning project; using more training data, synthetic data, or any new data captured from additional data source feeds.





